分饼干

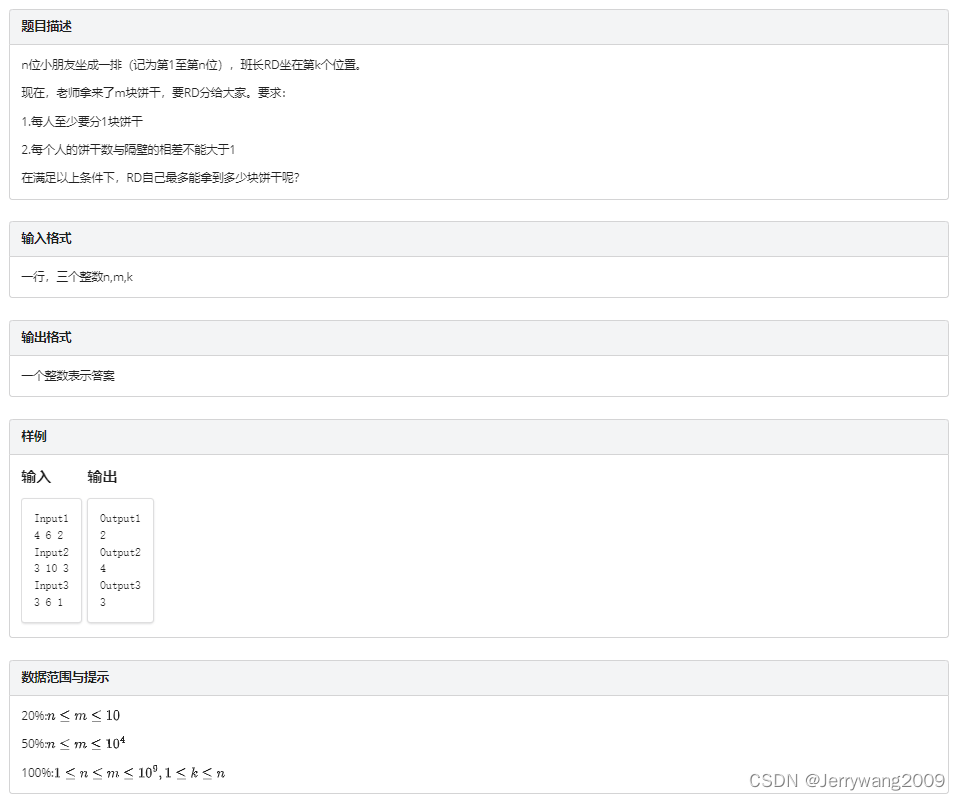
解析

无需二分，使用纯粹的数学就可以以 $O(1)$$O(1)$ 的时间复杂度解决。

先将 $m$$m$ 减去 $n$$n$，也就是给每个人先发 $1$$1$ 颗糖果。

设班长拿了 $x$$x$ 块糖，左边有 $l$$l$ 个人，右边有 $r$$r$ 个人。贪心地考虑发糖情况，类似于一个金字塔一样，最好左右都构成公差为 $1$$1$ 的等差数列。以下分情况假设，分别列出方程进行求解，并验证答案是否符合假设。

1. $x>l\mathrm{and}x>r$$x>l \operatorname{and} x>r$

   $$\begin{array}{c}\frac{(x-1+x-l)l+(x-1+x-r)r}{2}+x=m\\ 2xl-l^2-l+2xr-r^2-r+2x=2m\\ 2xl+2xr+2x=2m+l^2+r^2+l+r\\ x(2l+2r+2)=2m+l^2+r^2+l+r\\ x=\frac{2m+l^2+r^2+l+r}{2l+2r+2}\end{array}$$

   特别注意等差数列的末项是 $x-1$$x-1$，首项是 $x-l$$x-l$ 和 $x-r$$x-r$，项数是 $l$$l$ 或 $r$$r$。直接使用等差数列求和公式即可。

2. $x\le l\mathrm{and}x>r$$x\leq l \operatorname{and} x>r$

   $$\begin{array}{c}\frac{x(x-1)+(x-1+x-r)r}{2}+x=m\\ x^2-x+2xr-r-r^2+2x=2m\\ 2xr-r^2+x^2+x-r=2m\\ x^2+x(1+2r)-(2m+r+r^2)=0\end{array}$$

   对于以上的方程，直接使用一元二次方程求根公式求解即可。注意：两个解只须保留较大的，因为只需计算非负解。

3. $x\le r\mathrm{and}x>l$$x\leq r \operatorname{and} x>l$

   和情况 2 大同小异。

4. $x\le l\mathrm{and}x\le r$$x\leq l \operatorname{and} x\leq r$

   $$\begin{array}{c}\frac{x(x-1)}{2}\times 2+x=m\\ x^2-x+x=m\\ x^2=m\\ x=\sqrt{m}\end{array}$$

   对于以上的每个可行解，将解向下取整后打擂台求最大值即可。最后不要忘了，每个人先发了 $1$$1$ 颗糖果，$Max$$Max$ 值要加 $1$$1$。

    

代码

​x
// D
#include <bits/stdc++.h>
#define int long long
#define SIZE 200010
#define all(x) x.begin(), x.end()
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;

double solvex(int a, int b, int c)
{
    int x1=(-b+sqrt(b*b-4*a*c))*1.0/2*a;
    int x2=(-b-sqrt(b*b-4*a*c))*1.0/2*a;
    return max(x1, x2);
}

signed main()
{
    int n, m, k; cin>>n>>m>>k;
    m-=n;
    int s=0;
    int l=k-1;
    int r=n-l-1;
    int Max=0;
    // case 1: x>l && x>r
    double x=(int)(2*m+l*l+r*r+l+r)*1.0/(2*l+2*r+2);
    if(x>l && x>r)
        Max=max(Max, (int)x);
    // case 2: x<=l && x>r
    x=(int)solvex(1, 1+2*r, -(2*m+r+r*r));
    if(x>0 && x<=l && x>r)
        Max=max(Max, (int)x);
    // case 3: x>l && x<=r
    x=(int)solvex(1, 1+2*l, -(2*m+l+l*l));
    if(x>0 && x>l && x<=r)
        Max=max(Max, (int)x);
    // case 4: x<=l && x<=r
    x=(int)sqrt(m);
    if(x<=l && x<=r)
        Max=max(Max, (int)x);
    cout<<(int)(Max+1)<<endl;

    return 0;
}